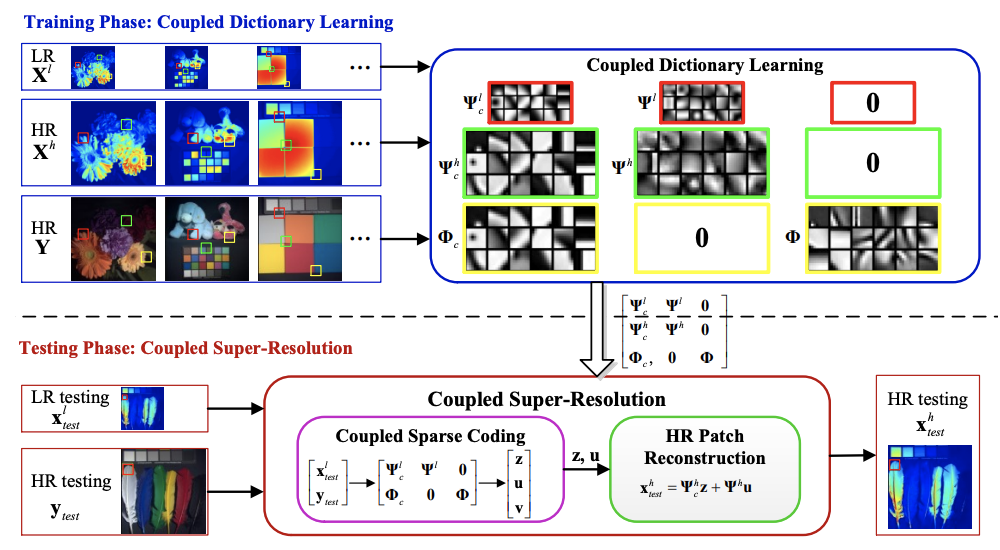
Abstract: Real-world data processing problems often involve various image modalities associated with a certain scene, including RGB images, infrared images or multi-spectral images. The fact that different image modalities often share certain attributes, such as edges, textures and other structure primitives, represents an opportunity to enhance various image processing tasks. This paper proposes a new approach to construct a high-resolution (HR) version of a low-resolution (LR) image given another HR image modality as guidance, based on joint sparse representations induced by coupled dictionaries. The proposed approach captures complex dependency correlations, including similarities and disparities, between different image modalities in a learned sparse feature domain in lieu of the original image domain. It consists of two phases: coupled dictionary learning phase and coupled super-resolution phase. The learning phase learns a set of dictionaries from the training dataset to couple different image modalities together in the sparse feature domain. In turn, the super-resolution phase leverages such dictionaries to construct a HR version of the LR target image with another related image modality for guidance. In the advanced version of our approach, multi-stage strategy and neighbourhood regression concept are introduced to further improve the model capacity and performance. Extensive guided image super-resolution experiments on real multimodal images demonstrate that the proposed approach admits distinctive advantages with respect to the state-of-the-art approaches, for example, overcoming the texture copying artifacts commonly resulting from inconsistency between the guidance and target images. Of particular relevance, the proposed model demonstrates much better robustness than competing deep models in a range of noisy scenarios.

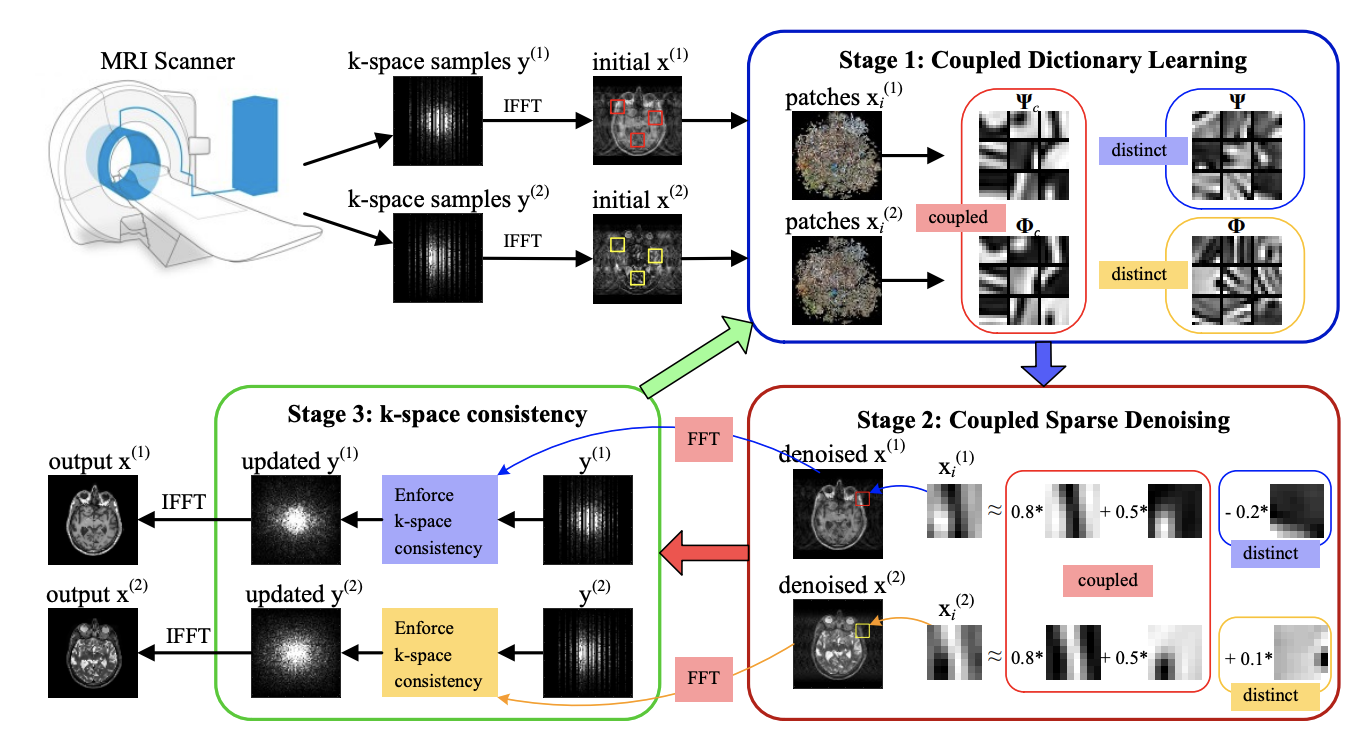
Abstract: Magnetic resonance (MR) imaging tasks often involve multiple contrasts, such as T1-weighted, T2-weighted and Fluid-attenuated inversion recovery (FLAIR) data. These contrasts capture information associated with the same underlying anatomy and thus exhibit similarities in either structure level or gray level. In this paper, we propose a Coupled Dictionary Learning based multi-contrast MRI reconstruction (CDLMRI) approach to leverage the dependency correlation between different contrasts for guided or joint reconstruction from their under-sampled k-space data. Our approach iterates between three stages: coupled dictionary learning, coupled sparse denoising, and enforcing k-space consistency. The first stage learns a set of dictionaries that not only are adaptive to the contrasts, but also capture correlations among multiple contrasts in a sparse transform domain. By capitalizing on the learned dictionaries, the second stage performs coupled sparse coding to remove the aliasing and noise in the corrupted contrasts. The third stage enforces consistency between the denoised contrasts and the measurements in the k-space domain. Numerical experiments, consisting of retrospective under-sampling of various MRI contrasts with a variety of sampling schemes, demonstrate that CDLMRI is capable of capturing structural dependencies between different contrasts. The learned priors indicate notable advantages in multi-contrast MR imaging and promising applications in quantitative MR imaging such as MR fingerprinting.

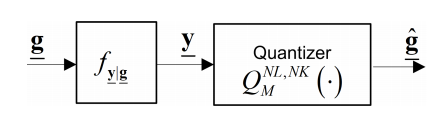
Abstract: Quantization plays a critical role in digital signal processing systems. Quantizers are typically designed to obtain an accurate digital representation of the input signal, operating independently of the system task, and are commonly implemented using serial scalar analog-to-digital converters (ADCs). In this work, we study hardware-limited task-based quantization, where a system utilizing a serial scalar ADC is designed to provide a suitable representation in order to allow the recovery of a parameter vector underlying the input signal. We propose hardware-limited task-based quantization systems for a fixed and finite quantization resolution, and characterize their achievable distortion. We then apply the analysis to the practical setups of channel estimation and eigen-spectrum recovery from quantized measurements. Our results illustrate that properly designed hardware-limited systems can approach the optimal performance achievable with vector quantizers, and that by taking the underlying task into account, the quantization error can be made negligible with a relatively small number of bits.

Abstract: Quantizers take part in nearly every digital signal processing system which operates on physical signals. They are commonly designed to accurately represent the underlying signal, regardless of the specific task to be performed on the quantized data. In systems working with high-dimensional signals, such as massive multiple-input multiple-output (MIMO) systems, it is beneficial to utilize low-resolution quantizers, due to cost, power, and memory constraints. In this work we study quantization of high-dimensional inputs, aiming at improving performance under resolution constraints by accounting for the system task in the quantizers design. We focus on the task of recovering a desired signal statistically related to the high-dimensional input, and analyze two quantization approaches: We first consider vector quantization, which is typically computationally infeasible, and characterize the optimal performance achievable with this approach. Next, we focus on practical systems which utilize hardware-limited scalar uniform analog-to-digital converters (ADCs), and design a taskbased quantizer under this model. The resulting system accounts for the task by linearly combining the observed signal into a lower dimension prior to quantization. We then apply our proposed technique to channel estimation in massive MIMO networks. Our results demonstrate that a system utilizing low-resolution scalar ADCs can approach the optimal channel estimation performance by properly accounting for the task in the system design.

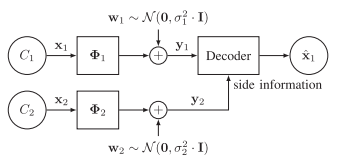
Abstract: This paper studies how to optimally capture side information to aid in the reconstruction of high-dimensional signals from low-dimensional random linear and noisy measurements, by assuming that both the signal of interest and the side information signal are drawn from a joint Gaussian mixture model. In particular, we derive sufficient and (occasionally) necessary conditions on the number of linear measurements for the signal reconstruction minimum mean squared error (MMSE) to approach zero in the low-noise regime; moreover, we also derive closed-form linear side information measurement designs for the reconstruction MMSE to approach zero in the low-noise regime. Our designs suggest that a linear projection kernel that optimally captures side information is such that it measures the attributes of side information that are maximally correlated with the signal of interest. A number of experiments both with synthetic and real data confirm that our theoretical results are well aligned with numerical ones. Finally, we offer a case study associated with a panchromatic sharpening (pan sharpening) application in the presence of compressive hyperspectral data that demonstrates that our proposed linear side information measurement designs can lead to reconstruction peak signal-to-noise ratio (PSNR) gains in excess of 2 dB over other approaches in this practical application.

Abstract: The generalization error of deep neural networks via their classification margin is studied in this work. Our approach is based on the Jacobian matrix of a deep neural network and can be applied to networks with arbitrary non-linearities and pooling layers, and to networks with different architectures such as feed forward networks and residual networks. Our analysis leads to the conclusion that a bounded spectral norm of the network's Jacobian matrix in the neighbourhood of the training samples is crucial for a deep neural network of arbitrary depth and width to generalize well. This is a significant improvement over the current bounds in the literature, which imply that the generalization error grows with either the width or the depth of the network. Moreover, it shows that the recently proposed batch normalization and weight normalization re-parametrizations enjoy good generalization properties, and leads to a novel network regularizer based on the network's Jacobian matrix. The analysis is supported with experimental results on the MNIST, CIFAR-10, LaRED and ImageNet datasets.

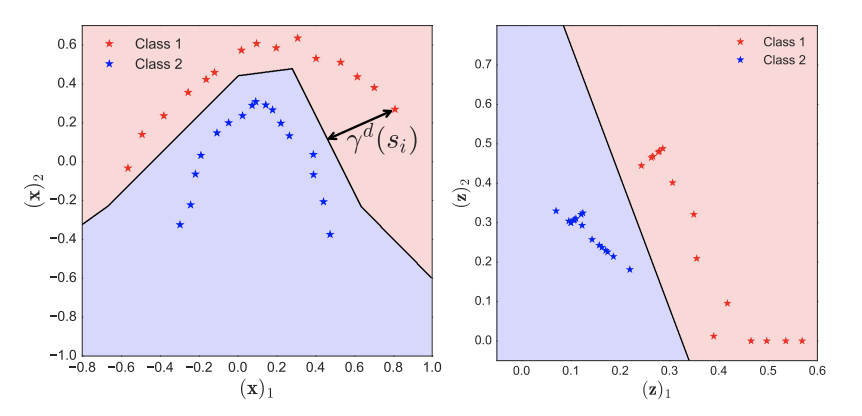
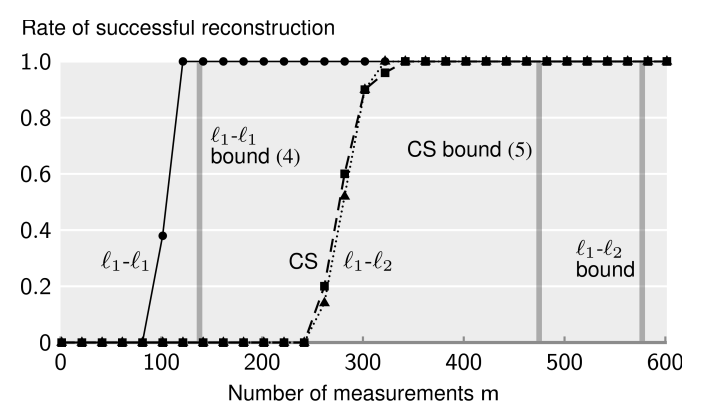
Abstract: We address the problem of compressed sensing (CS) with prior information: reconstruct a target CS signal with the aid of a similar signal that is known beforehand, our prior information. We integrate the additional knowledge of the similar signal into CS via l 1 -l 1 and l 1 -l 2 minimization. We then establish bounds on the number of measurements required by these problems to successfully reconstruct the original signal. Our bounds and geometrical interpretations reveal that if the prior information has good enough quality, l 1 -l 1 minimization improves the performance of CS dramatically. In contrast, l 1 -l 2 minimization has a performance very similar to classical CS, and brings no significant benefits. In addition, we use the insight provided by our bounds to design practical schemes to improve prior information. All our findings are illustrated with experimental results.

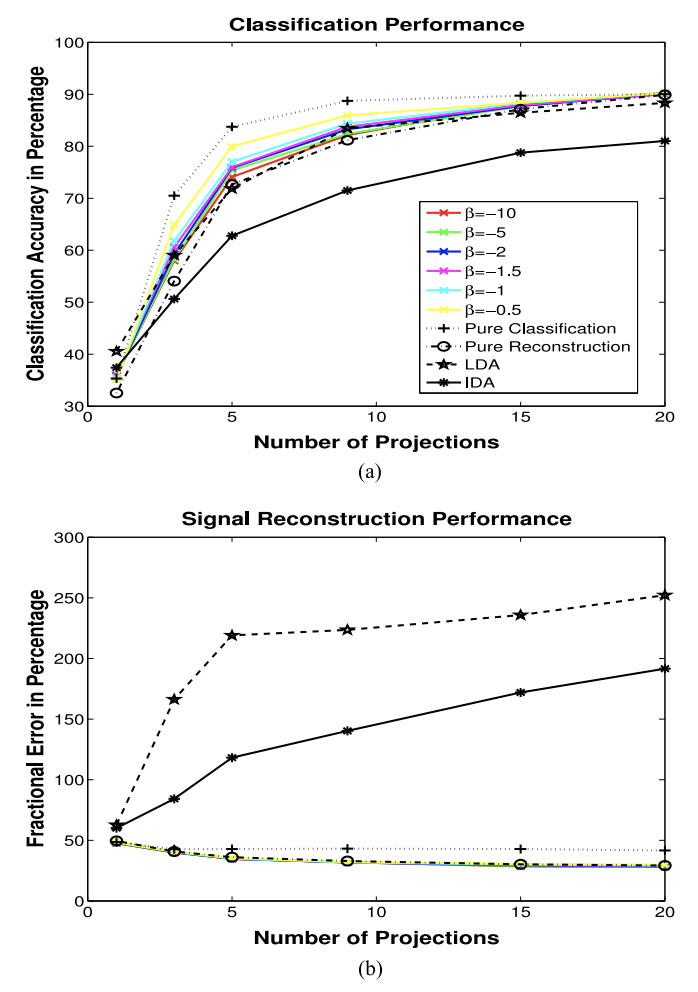
Abstract: An information-theoretic projection design framework is proposed, of interest for feature design and compressive measurements. Both Gaussian and Poisson measurement models are considered. The gradient of a proposed information-theoretic metric (ITM) is derived, and a gradient-descent algorithm is applied in design; connections are made to the information bottleneck. The fundamental solution structure of such design is revealed in the case of a Gaussian measurement model and arbitrary input statistics. This new theoretical result reveals how ITM parameter settings impact the number of needed projection measurements, with this verified experimentally. The ITM achieves promising results on real data, for both signal recovery and classification.

Abstract: In support of art investigation, we propose a new source separation method that unmixes a single X-ray scan acquired from double-sided paintings. In this problem, the X-ray signals to be separated have similar morphological characteristics, which brings previous source separation methods to their limits. Our solution is to use photographs taken from the front-and back-side of the panel to drive the separation process. The crux of our approach relies on the coupling of the two imaging modalities (photographs and X-rays) using a novel coupled dictionary learning framework able to capture both common and disparate features across the modalities using parsimonious representations; the common component captures features shared by the multi-modal images, whereas the innovation component captures modality-specific information. As such, our model enables the formulation of appropriately regularized convex optimization procedures that lead to the accurate separation of the X-rays. Our dictionary learning framework can be tailored both to a single- and a multi-scale framework, with the latter leading to a significant performance improvement. Moreover, to improve further on the visual quality of the separated images, we propose to train coupled dictionaries that ignore certain parts of the painting corresponding to craquelure. Experimentation on synthetic and real data - taken from digital acquisition of the Ghent Altarpiece (1432) - confirms the superiority of our method against the state-of-the-art morphological component analysis technique that uses either fixed or trained dictionaries to perform image separation.

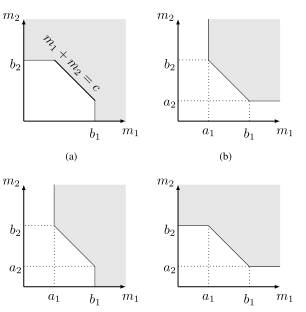
Abstract: This paper offers a characterization of fundamental limits on the classification and reconstruction of high-dimensional signals from low-dimensional features, in the presence of side information. We consider a scenario where a decoder has access both to linear features of the signal of interest and to linear features of the side information signal; while the side information may be in a compressed form, the objective is recovery or classification of the primary signal, not the side information. The signal of interest and the side information are each assumed to have (distinct) latent discrete labels; conditioned on these two labels, the signal of interest and side information are drawn from a multivariate Gaussian distribution that correlates the two. With joint probabilities on the latent labels, the overall signal-(side information) representation is defined by a Gaussian mixture model. By considering bounds to the misclassification probability associated with the recovery of the underlying signal label, and bounds to the reconstruction error associated with the recovery of the signal of interest itself, we then provide sharp sufficient and/or necessary conditions for these quantities to approach zero when the covariance matrices of the Gaussians are nearly low rank. These conditions, which are reminiscent of the well-known Slepian-Wolf and Wyner-Ziv conditions, are the function of the number of linear features extracted from signal of interest, the number of linear features extracted from the side information signal, and the geometry of these signals and their interplay. Moreover, on assuming that the signal of interest and the side information obey such an approximately low-rank model, we derive the expansions of the reconstruction error as a function of the deviation from an exactly low-rank model; such expansions also allow the identification of operational regimes, where the impact of side information on signal reconstruction is most relevant. Our framework, which offers a principled mechanism to integrate side information in high-dimensional data problems, is also tested in the context of imaging applications. In particular, we report state-of-theart results in compressive hyperspectral imaging applications, where the accompanying side information is a conventional digital photograph..

Abstract: This paper studies the classification of high-dimensional Gaussian signals from low-dimensional noisy, linear measurements. In particular, it provides upper bounds (sufficient conditions) on the number of measurements required to drive the probability of misclassification to zero in the low-noise regime, both for random measurements and designed ones. Such bounds reveal two important operational regimes that are a function of the characteristics of the source: 1) when the number of classes is less than or equal to the dimension of the space spanned by signals in each class, reliable classification is possible in the low-noise regime by using a one-vs-all measurement design; 2) when the dimension of the spaces spanned by signals in each class is lower than the number of classes, reliable classification is guaranteed in the low-noise regime by using a simple random measurement design. Simulation results both with synthetic and real data show that our analysis is sharp, in the sense that it is able to gauge the number of measurements required to drive the misclassification probability to zero in the low-noise regime.

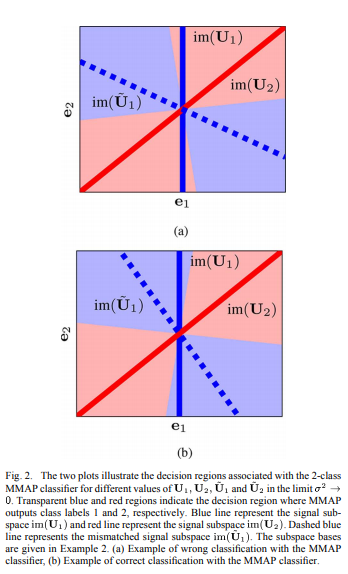
Abstract: This paper considers the classification of linear subspaces with mismatched classifiers. In particular, we assume a model where one observes signals in the presence of isotropic Gaussian noise and the distribution of the signals conditioned on a given class is Gaussian with a zero mean and a low-rank covariance matrix. We also assume that the classifier knows only a mismatched version of the parameters of input distribution in lieu of the true parameters. By constructing an asymptotic low-noise expansion of an upper bound to the error probability of such a mismatched classifier, we provide sufficient conditions for reliable classification in the low-noise regime that are able to sharply predict the absence of a classification error floor. Such conditions are a function of the geometry of the true signal distribution, the geometry of the mismatched signal distributions as well as the interplay between such geometries, namely, the principal angles and the overlap between the true and the mismatched signal subspaces. Numerical results demonstrate that our conditions for reliable classification can sharply predict the behavior of a mismatched classifier both with synthetic data and in a motion segmentation and a hand-written digit classification applications.

Abstract: Repurposing tools and intuitions from Shannon theory, we derive fundamental limits on the reliable classification of high-dimensional signals from low-dimensional features. We focus on the classification of linear and affine subspaces and suppose the features to be noisy linear projections. Leveraging a syntactic equivalence of discrimination between subspaces and communications over vector wireless channels, we derive asymptotic bounds on classifier performance. First, we define the classification capacity, which characterizes necessary and sufficient relationships between the signal dimension, the number of features, and the number of classes to be discriminated, as all three quantities approach infinity. Second, we define the diversitydiscrimination tradeoff, which characterizes relationships between the number of classes and the misclassification probability as the signal-to-noise ratio approaches infinity. We derive inner and outer bounds on these measures, revealing precise relationships between signal dimension and classifier performance.

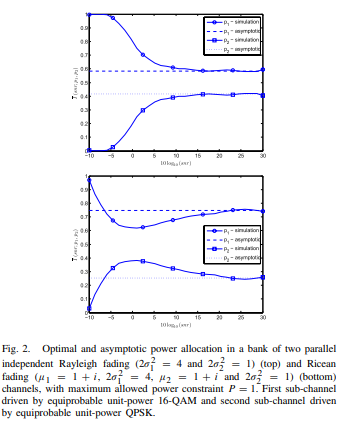
Abstract: We consider the characterization of the asymptotic behavior of the average minimum mean-squared error (MMSE) in scalar and vector fading coherent channels, where the receiver knows the exact fading channel state but the transmitter knows only the fading channel distribution, driven by a range of inputs. In particular, we construct expansions of the quantities that are asymptotic in the signal-to-noise ratio (snr) for coherent channels subject to Rayleigh, Ricean or Nakagami fading and driven by discrete inputs and continuous inputs. The construction of these expansions leverages the fact that the average MMSE can be seen as an ψ-transform with a kernel of monotonic argument: this offers the means to use a powerful asymptotic expansion of integrals technique-the Mellin transform method-that leads immediately to the expansions of the average MMSE and- via the I-MMSE relationship-to expansions of the average mutual information, in terms of the so called canonical MMSE of a standard additive white Gaussian noise (AWGN) channel. We conclude with applications of the results to the optimization of the constrained capacity of a bank of parallel independent coherent fading channels driven by arbitrary discrete inputs.

Abstract: A generalization of Bregman divergence is developed and utilized to unify vector Poisson and Gaussian channel models, from the perspective of the gradient of mutual information. The gradient is with respect to the measurement matrix in a compressive-sensing setting, and mutual information is considered for signal recovery and classification. Existing gradient-of-mutual-information results for scalar Poisson models are recovered as special cases, as are known results for the vector Gaussian model. The Bregman-divergence generalization yields a Bregman matrix, and this matrix induces numerous matrix-valued metrics. The metrics associated with the Bregman matrix are detailed, as are its other properties. The Bregman matrix is also utilized to connect the relative entropy and mismatched minimum mean squared error. Two applications are considered: 1) compressive sensing with a Poisson measurement model and 2) compressive topic modeling for analysis of a document corpora (word-count data). In both of these settings, we use the developed theory to optimize the compressive measurement matrix, for signal recovery and classification.

Abstract: This paper determines to within a single measurement the minimum number of measurements required to successfully reconstruct a signal drawn from a Gaussian mixture model in the low-noise regime. The method is to develop upper and lower bounds that are a function of the maximum dimension of the linear subspaces spanned by the Gaussian mixture components. The method not only reveals the existence or absence of a minimum mean-squared error (MMSE) error floor (phase transition) but also provides insight into the MMSE decay via multivariate generalizations of the MMSE dimension and the MMSE power offset, which are a function of the interaction between the geometrical properties of the kernel and the Gaussian mixture. These results apply not only to standard linear random Gaussian measurements but also to linear kernels that minimize the MMSE. It is shown that optimal kernels do not change the number of measurements associated with the MMSE phase transition, rather they affect the sensed power required to achieve a target MMSE in the low-noise regime. Overall, our bounds are tighter and sharper than standard bounds on the minimum number of measurements needed to recover sparse signals associated with a union of subspaces model, as they are not asymptotic in the signal dimension or signal sparsity.

Abstract: This paper determines to within a single measurement the minimum number of measurements required to successfully reconstruct a signal drawn from a Gaussian mixture model in the low-noise regime. The method is to develop upper and lower bounds that are a function of the maximum dimension of the linear subspaces spanned by the Gaussian mixture components. The method not only reveals the existence or absence of a minimum mean-squared error (MMSE) error floor (phase transition) but also provides insight into the MMSE decay via multivariate generalizations of the MMSE dimension and the MMSE power offset, which are a function of the interaction between the geometrical properties of the kernel and the Gaussian mixture. These results apply not only to standard linear random Gaussian measurements but also to linear kernels that minimize the MMSE. It is shown that optimal kernels do not change the number of measurements associated with the MMSE phase transition, rather they affect the sensed power required to achieve a target MMSE in the low-noise regime. Overall, our bounds are tighter and sharper than standard bounds on the minimum number of measurements needed to recover sparse signals associated with a union of subspaces model, as they are not asymptotic in the signal dimension or signal sparsity.

Abstract: This paper considers the problem of filter design with secrecy constraints, where two legitimate parties (Alice and Bob) communicate in the presence of an eavesdropper (Eve), over a Gaussian multiple-input-multiple-output (MIMO) wiretap channel. This problem involves designing, subject to a power constraint, the transmit and the receive filters which minimize the mean-squared error (MSE) between the legitimate parties whilst assuring that the eavesdropper MSE remains above a certain threshold. We consider a general MIMO Gaussian wiretap scenario, where the legitimate receiver uses a linear Zero-Forcing (ZF) filter and the eavesdropper receiver uses either a ZF or an optimal linear Wiener filter. We provide a characterization of the optimal filter designs by demonstrating the convexity of the optimization problems. We also provide generalizations of the filter designs from the scenario where the channel state is known to all the parties to the scenario where there is uncertainty in the channel state. A set of numerical results illustrates the performance of the novel filter designs, including the robustness to channel modeling errors. In particular, we assess the efficacy of the designs in guaranteeing not only a certain MSE level at the eavesdropper, but also in limiting the error probability at the eavesdropper. We also assess the impact of the filter designs on the achievable secrecy rates. The penalty induced by the fact that the eavesdropper may use the optimal non-linear receive filter rather than the optimal linear one is also explored in the paper.

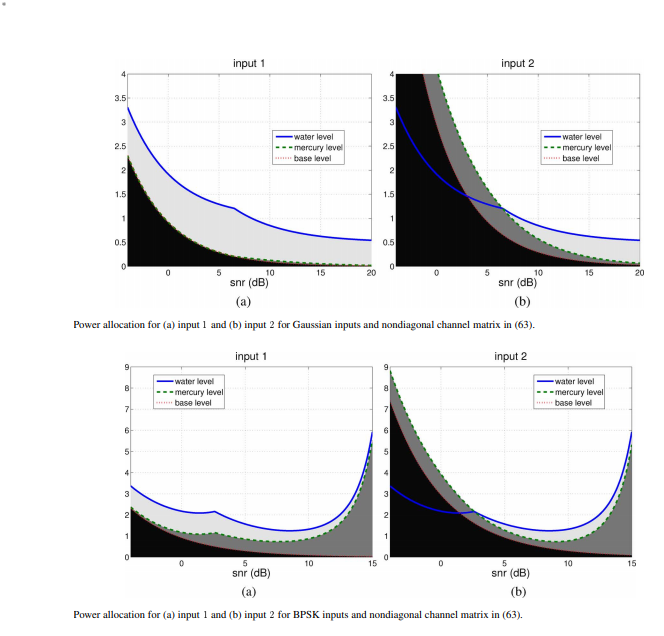
Abstract: In this paper, we investigate the linear precoding and power allocation policies that maximize the mutual information for general multiple-input-multiple-output (MIMO) Gaussian channels with arbitrary input distributions, by capitalizing on the relationship between mutual information and minimum mean-square error (MMSE). The optimal linear precoder satisfies a fixed-point equation as a function of the channel and the input constellation. For non-Gaussian inputs, a nondiagonal precoding matrix in general increases the information transmission rate, even for parallel noninteracting channels. Whenever precoding is precluded, the optimal power allocation policy also satisfies a fixed-point equation; we put forth a generalization of the mercury/waterfilling algorithm, previously proposed for parallel noninterfering channels, in which the mercury level accounts not only for the non-Gaussian input distributions, but also for the interference among inputs.

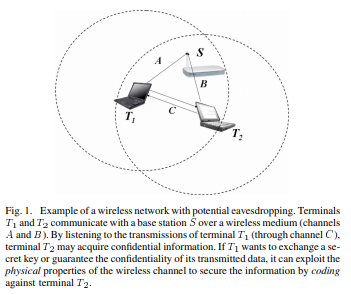
Abstract: This paper considers the transmission of confidential data over wireless channels. Based on an information-theoretic formulation of the problem, in which two legitimates partners communicate over a quasi-static fading channel and an eavesdropper observes their transmissions through a second independent quasi-static fading channel, the important role of fading is characterized in terms of average secure communication rates and outage probability. Based on the insights from this analysis, a practical secure communication protocol is developed, which uses a four-step procedure to ensure wireless information-theoretic security: (i) common randomness via opportunistic transmission, (ii) message reconciliation, (iii) common key generation via privacy amplification, and (iv) message protection with a secret key. A reconciliation procedure based on multilevel coding and optimized low-density parity-check (LDPC) codes is introduced, which allows to achieve communication rates close to the fundamental security limits in several relevant instances. Finally, a set of metrics for assessing average secure key generation rates is established, and it is shown that the protocol is effective in secure key renewal-even in the presence of imperfect channel state information.