Jaweria Amjad
Previous PhD Student

Contact
Where to Find Me
Malet Place Engineering Building
Torrington Place
London WC1E 7JE
United Kingdom
My Feed
Tweets by Jaweria
Research Interests
I am interested in the generalization and optimisation of Deep learning solvers for Linear inverse problems in imaging.
About
I am currently a fourth-year PhD student in the Electronics & Electrical Engineering Department, University College London, supervised by Professor Miguel R. D. Rodrigues. Before this, I was a lecturer in CIIT, Pakistan. I obtained my MS and BS from the National University of Science and Technology, Pakistan in 2012 and 2009 respectively
Publications
2019
Authors: J. Amjad, Z. Lyu, M. R. D. Rodrigues
Journal/Conference: arXiv pre-print
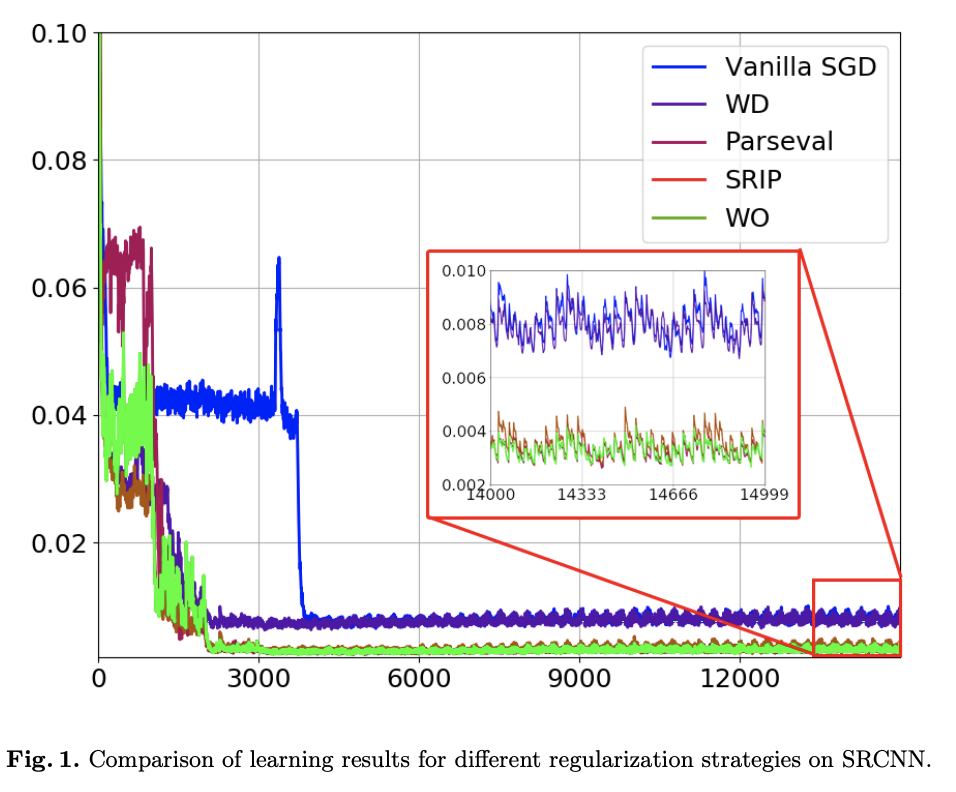
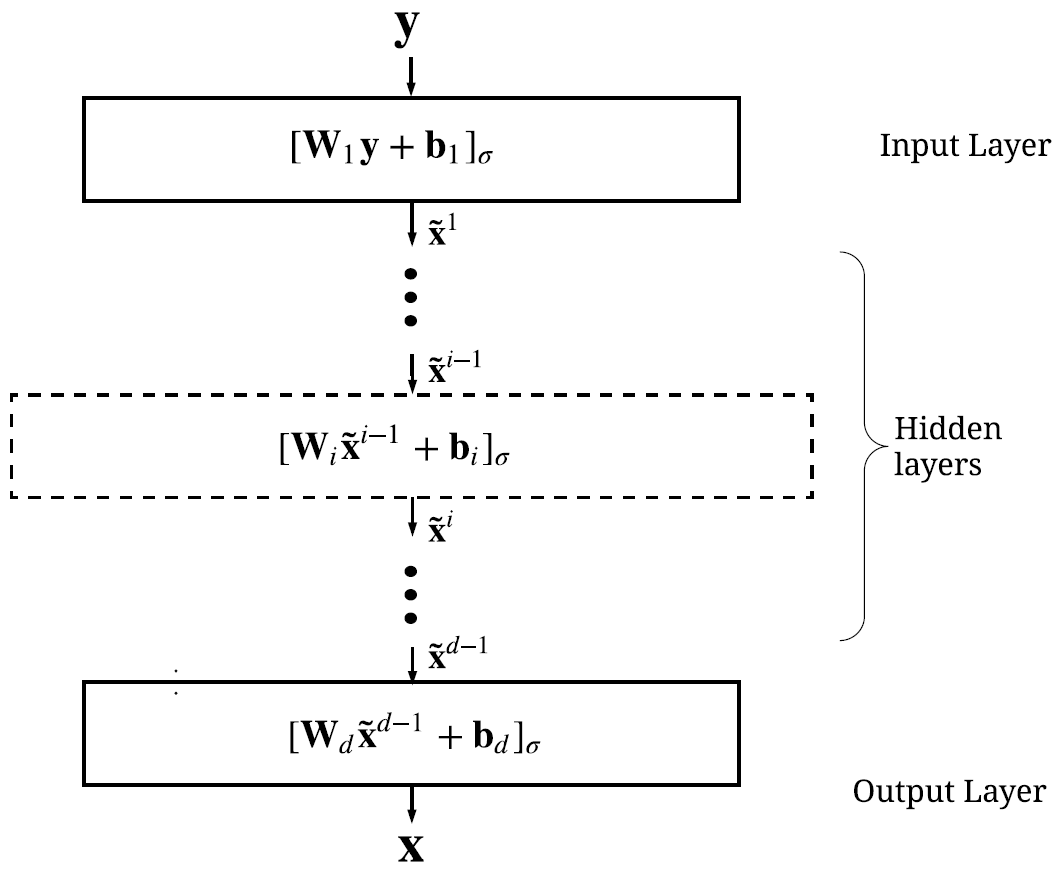
Abstract: Inverse problems abound in a number of domains such as medical imaging, remote sensing, and many more, relying on the use of advanced signal & image processing approaches – such as sparsity-driven techniques – to determine their solution. This paper instead studies the use of deep learning approaches to approximate the solution of inverse problems. In particular, the paper provides a new generalization bound, depending on key quantity associated with a deep neural network – its Jacobian matrix – that also leads to a number of computationally efficient regularization strategies applicable to inverse problems The paper also tests the proposed regularization strategies in a number of inverse problems including image super-resolution ones. Our numerical results conducted on various datasets show that both fully connected and convolutional neural networks regularized using the regularization or proxy regularization strategies originating from our theory exhibit much better performance than deep networks regularized with standard approaches such as weight-decay.
Link2018
Authors: J. Amjad, J. Sokolic, M. R. D. Rodrigues
Journal/Conference: European Signal Processing Conference (EUSIPCO) 2018
Abstract:This paper analyses the generalization behaviour of a deep neural networks with a focus on their use in inverse problems. In particular, by leveraging the robustness framework by Xu and Mannor, we provide deep neural network based regression generalization bounds that are also specialized to sparse approximation problems. The proposed bounds show that the sparse approximation performance of deep neural networks can be potentially superior to that of classical sparse reconstruction algorithms, with reconstruction errors limited only by the noise level independently of the underlying data.
Link